深入探討機率圖¶

概述¶

probscale.probplot 函數可讓您執行幾項操作。它們是

建立百分位數、分位數或機率圖。
將您的機率尺度放置在任一軸上。
為您的機率尺度指定任意分佈。
在線性機率或對數機率空間中繪製最佳擬合線。
以您想要的任何方式計算您的資料的繪圖位置。
在 seaborn FacetGrids 上使用機率軸

我們將在本教學中介紹所有這些選項。

%matplotlib inline

import warnings
warnings.simplefilter('ignore')

import numpy
from matplotlib import pyplot
import seaborn

import probscale
clear_bkgd = {'axes.facecolor':'none', 'figure.facecolor':'none'}
seaborn.set(style='ticks', context='talk', color_codes=True, rc=clear_bkgd)

# load up some example data from the seaborn package
tips = seaborn.load_dataset("tips")
iris = seaborn.load_dataset("iris")

不同的圖表類型¶

一般而言，有三種圖表類型

百分位數，又名 P-P 圖
分位數，又名 Q-Q 圖
機率，又名機率圖

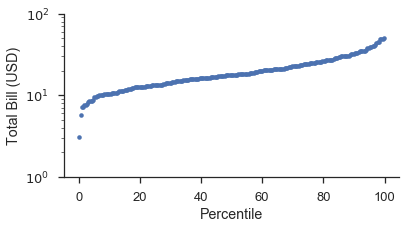
百分位數圖¶

百分位數圖是最簡單的圖。您只需將資料繪製在其繪圖位置上即可。繪圖位置顯示在線性尺度上，但資料可以根據需要進行縮放。

如果您從頭開始做，它看起來會像這樣

position, bill = probscale.plot_pos(tips['total_bill'])
position *= 100
fig, ax = pyplot.subplots(figsize=(6, 3))
ax.plot(position, bill, marker='.', linestyle='none', label='Bill amount')
ax.set_xlabel('Percentile')
ax.set_ylabel('Total Bill (USD)')
ax.set_yscale('log')
ax.set_ylim(bottom=1, top=100)
seaborn.despine()

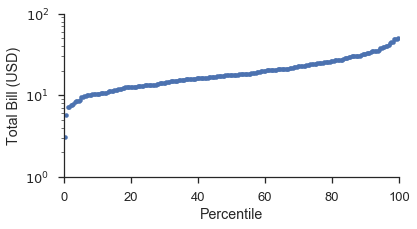
使用 probplot 函數和 plottype='pp'，它變成

fig, ax = pyplot.subplots(figsize=(6, 3))
fig = probscale.probplot(tips['total_bill'], ax=ax, plottype='pp', datascale='log',
                         problabel='Percentile', datalabel='Total Bill (USD)',
                         scatter_kws=dict(marker='.', linestyle='none', label='Bill Amount'))
ax.set_ylim(bottom=1, top=100)
seaborn.despine()

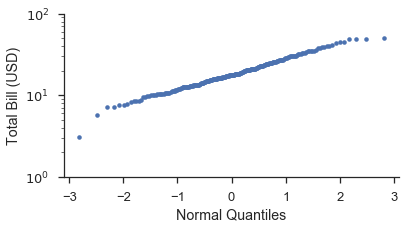
分位數圖¶

分位數圖與機率圖相似。主要差異在於，繪圖位置會根據機率分佈轉換為分位數或 \(Z\) 分數。預設分佈是標準常態分佈。使用不同的分佈將在稍後介紹。

使用與上面相同的資料集，讓我們建立一個分位數圖。如同上面，我們先從頭開始做，然後再使用 probplot。

from scipy import stats

position, bill = probscale.plot_pos(tips['total_bill'])
quantile = stats.norm.ppf(position)

fig, ax = pyplot.subplots(figsize=(6, 3))
ax.plot(quantile, bill, marker='.', linestyle='none', label='Bill amount')
ax.set_xlabel('Normal Quantiles')
ax.set_ylabel('Total Bill (USD)')
ax.set_yscale('log')
ax.set_ylim(bottom=1, top=100)
seaborn.despine()

使用 probplot

fig, ax = pyplot.subplots(figsize=(6, 3))
fig = probscale.probplot(tips['total_bill'], ax=ax, plottype='qq', datascale='log',
                         problabel='Standard Normal Quantiles', datalabel='Total Bill (USD)',
                         scatter_kws=dict(marker='.', linestyle='none', label='Bill Amount'))

ax.set_ylim(bottom=1, top=100)
seaborn.despine()

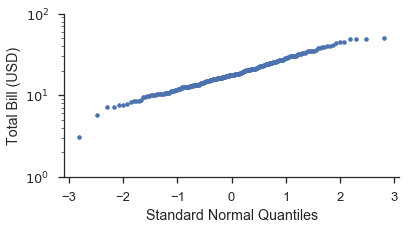
您會注意到，在 Q-Q 圖上，資料的形狀比在 P-P 圖上更直。這是因為將繪圖位置轉換為分佈的分位數時發生的轉換所導致的。下圖希望能更清楚地說明這一點。此外，我們將展示如何使用 probax 選項翻轉圖表，使 P-P/Q-Q/機率軸位於 y 尺度上。

fig, (ax1, ax2) = pyplot.subplots(figsize=(6, 6), ncols=2, sharex=True)
markers = dict(marker='.', linestyle='none', label='Bill Amount')

fig = probscale.probplot(tips['total_bill'], ax=ax1, plottype='pp', probax='y',
                         datascale='log', problabel='Percentiles',
                         datalabel='Total Bill (USD)', scatter_kws=markers)

fig = probscale.probplot(tips['total_bill'], ax=ax2, plottype='qq', probax='y',
                         datascale='log', problabel='Standard Normal Quantiles',
                         datalabel='Total Bill (USD)', scatter_kws=markers)

ax1.set_xlim(left=1, right=100)
fig.tight_layout()
seaborn.despine()

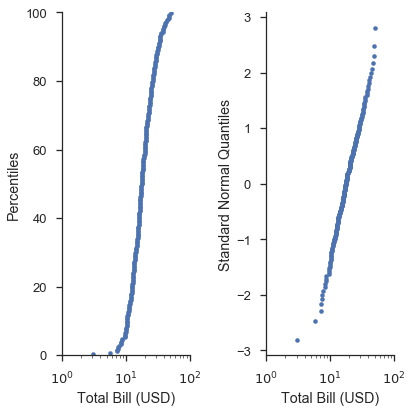
在 P-P 圖和簡單 Q-Q 圖的情況下，與編寫原始 matplotlib 命令相比，probplot 函數沒有提供太多便利性。但是，當您開始建立機率圖並使用更進階的選項時，這種情況會改變。

機率圖¶

在視覺上，機率和分位數尺度上的圖形曲線應相同。不同之處在於，軸刻度是根據非超越機率而不是分佈的更抽象分位數來放置和標記的。

毫不意外地，圖片能更好地解釋這一點。讓我們以前面的圖表為基礎

fig, (ax1, ax2, ax3) = pyplot.subplots(figsize=(9, 6), ncols=3, sharex=True)
common_opts = dict(
    probax='y',
    datascale='log',
    datalabel='Total Bill (USD)',
    scatter_kws=dict(marker='.', linestyle='none')
)

fig = probscale.probplot(tips['total_bill'], ax=ax1, plottype='pp',
                         problabel='Percentiles',  **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax2, plottype='qq',
                         problabel='Standard Normal Quantiles',  **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax3, plottype='prob',
                         problabel='Standard Normal Probabilities',  **common_opts)

ax3.set_xlim(left=1, right=100)
ax3.set_ylim(bottom=0.13, top=99.87)
fig.tight_layout()
seaborn.despine()

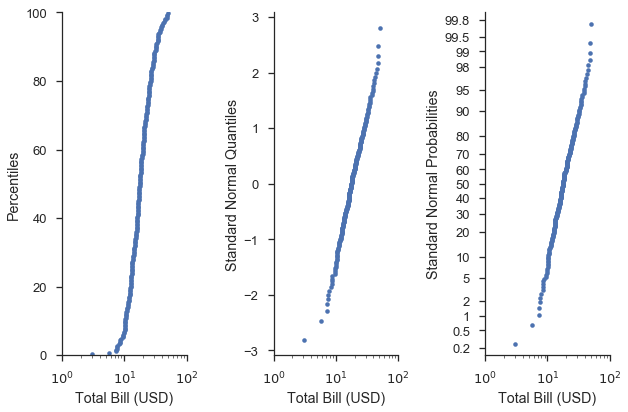
在視覺上，最右側圖表的曲線形狀是相同的。不同之處在於 y 軸刻度和標籤更「人性化」。

換句話說，機率（右）軸讓我們更容易找到例如在百分位數（左）軸上找到的第 75 個百分位數，並說明資料如何符合給定的分佈，如分位數（中間）軸所示。

為您的尺度使用不同的分佈¶

當使用分位數或機率尺度時，您可以將 scipy.stats 模組中的分佈傳遞給 probplot 函數。當未將分佈提供給 dist 參數時，將使用標準常態分佈。

common_opts = dict(
    plottype='prob',
    probax='y',
    datascale='log',
    datalabel='Total Bill (USD)',
    scatter_kws=dict(marker='+', linestyle='none', mew=1)
)

alpha = stats.alpha(10)
beta = stats.beta(6, 3)

fig, (ax1, ax2, ax3) = pyplot.subplots(figsize=(9, 6), ncols=3, sharex=True)
fig = probscale.probplot(tips['total_bill'], ax=ax1, dist=alpha,
                         problabel='Alpha(10) Probabilities', **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax2, dist=beta,
                         problabel='Beta(6, 1) Probabilities', **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax3, dist=None,
                         problabel='Standard Normal Probabilities', **common_opts)

ax3.set_xlim(left=1, right=100)
for ax in [ax1, ax2, ax3]:
    ax.set_ylim(bottom=0.2, top=99.8)
seaborn.despine()
fig.tight_layout()

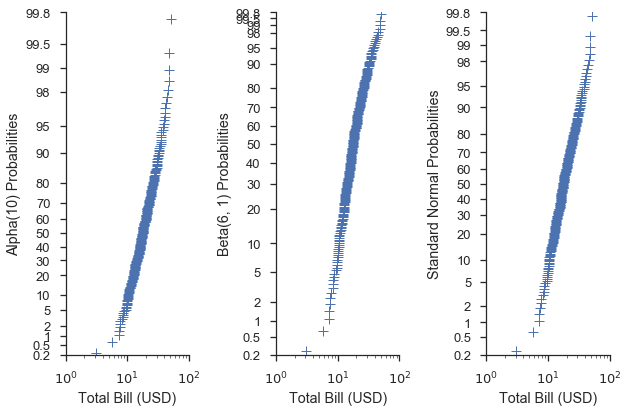
這也可以對 QQ 尺度執行

common_opts = dict(
    plottype='qq',
    probax='y',
    datascale='log',
    datalabel='Total Bill (USD)',
    scatter_kws=dict(marker='+', linestyle='none', mew=1)
)

alpha = stats.alpha(10)
beta = stats.beta(6, 3)

fig, (ax1, ax2, ax3) = pyplot.subplots(figsize=(9, 6), ncols=3, sharex=True)
fig = probscale.probplot(tips['total_bill'], ax=ax1, dist=alpha,
                         problabel='Alpha(10) Quantiles', **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax2, dist=beta,
                         problabel='Beta(6, 3) Quantiles', **common_opts)

fig = probscale.probplot(tips['total_bill'], ax=ax3, dist=None,
                         problabel='Standard Normal Quantiles', **common_opts)

ax1.set_xlim(left=1, right=100)
seaborn.despine()
fig.tight_layout()

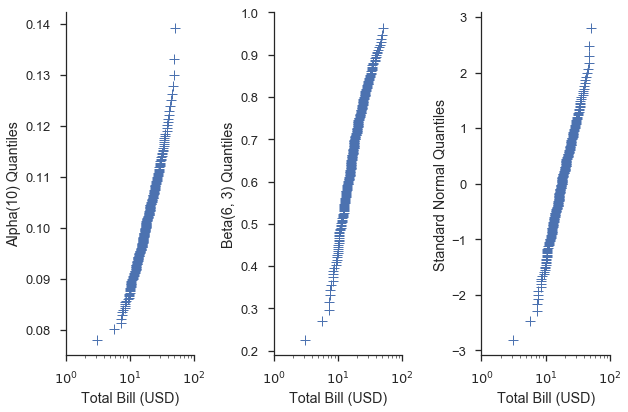
在分位數尺度上使用特定的分佈可以讓我們瞭解資料與該分佈的擬合程度。例如，假設我們有一個預感，我們的資料集中 total_bill 欄的值呈常態分佈，且其平均值和標準差分別為 19.8 和 8.9。我們可以透過建立一個具有這些參數的 scipy.stat.norm 分佈並在 Q-Q 圖中使用該分佈來研究這一點。

def equality_line(ax, label=None):
    limits = [
        numpy.min([ax.get_xlim(), ax.get_ylim()]),
        numpy.max([ax.get_xlim(), ax.get_ylim()]),
    ]
    ax.set_xlim(limits)
    ax.set_ylim(limits)
    ax.plot(limits, limits, 'k-', alpha=0.75, zorder=0, label=label)

norm = stats.norm(loc=21, scale=8)
fig, ax = pyplot.subplots(figsize=(5, 5))
ax.set_aspect('equal')

common_opts = dict(
    plottype='qq',
    probax='x',
    problabel='Theoretical Quantiles',
    datalabel='Emperical Quantiles',
    scatter_kws=dict(label='Bill amounts')
)

fig = probscale.probplot(tips['total_bill'], ax=ax, dist=norm, **common_opts)

equality_line(ax, label='Guessed Normal Distribution')
ax.legend(loc='lower right')
seaborn.despine()

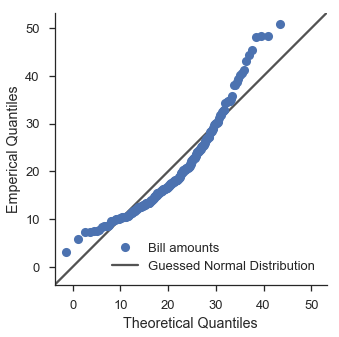
嗯。看起來不太好。讓我們使用 scipy 的擬合功能來嘗試對數常態分佈。

lognorm_params = stats.lognorm.fit(tips['total_bill'], floc=0)
lognorm = stats.lognorm(*lognorm_params)
fig, ax = pyplot.subplots(figsize=(5, 5))
ax.set_aspect('equal')

fig = probscale.probplot(tips['total_bill'], ax=ax, dist=lognorm, **common_opts)

equality_line(ax, label='Fit Lognormal Distribution')
ax.legend(loc='lower right')
seaborn.despine()

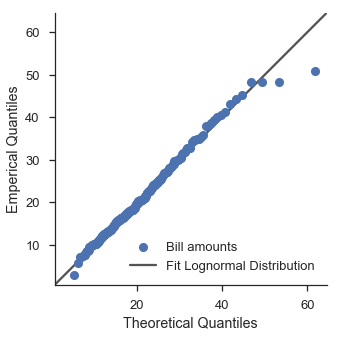
好一點了。

尋找最佳分佈作為讀者的練習。

最佳擬合線¶

在機率圖中加入最佳擬合線可以深入瞭解資料集是否可以透過分佈來描述。

這只需在 probplot 中使用 bestfit=True 選項即可完成。在幕後，probplot 會根據資料軸的圖表類型和尺度（透過 datascale 控制）轉換回歸的 x 和 y 資料。

可以使用 line_kws 參數控制線的視覺屬性。如果您想標記最佳擬合線，您可以在那裡指定其標籤。

簡單範例¶

最簡單的情況是具有線性資料軸的 P-P 圖

fig, ax = pyplot.subplots(figsize=(6, 3))
fig = probscale.probplot(tips['total_bill'], ax=ax, plottype='pp', bestfit=True,
                         problabel='Percentile', datalabel='Total Bill (USD)',
                         scatter_kws=dict(label='Bill Amount'),
                         line_kws=dict(label='Best-fit line'))
ax.legend(loc='upper left')
seaborn.despine()

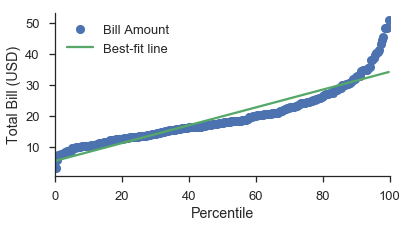
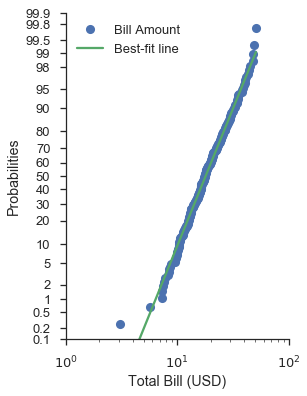
最不簡單的情況是具有對數尺度資料軸的機率圖。

如具有自訂分佈的分位數圖章節所示，使用對數常態資料尺度的一般常態機率尺度可提供良好的擬合（視覺上而言）。

請注意，您仍然將機率尺度放在 x 軸或 y 軸上。

fig, ax = pyplot.subplots(figsize=(4, 6))
fig = probscale.probplot(tips['total_bill'], ax=ax, plottype='prob', probax='y', bestfit=True,
                         datascale='log', problabel='Probabilities', datalabel='Total Bill (USD)',
                         scatter_kws=dict(label='Bill Amount'),
                         line_kws=dict(label='Best-fit line'))
ax.legend(loc='upper left')
ax.set_ylim(bottom=0.1, top=99.9)
ax.set_xlim(left=1, right=100)
seaborn.despine()

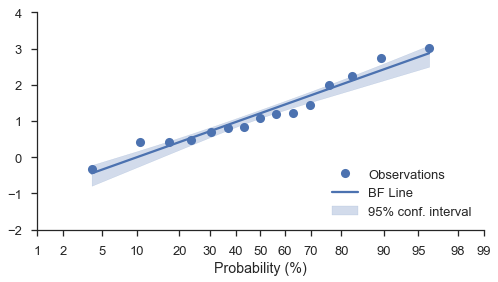
自舉信賴區間¶

無論圖表的尺度（線性、對數或機率）如何，您都可以在最佳擬合線周圍新增自舉信賴區間。只需使用 estimate_ci=True 選項以及 bestfit=True

N = 15
numpy.random.seed(0)
x = numpy.random.normal(size=N) + numpy.random.uniform(size=N)
fig, ax = pyplot.subplots(figsize=(8, 4))
fig = probscale.probplot(x, ax=ax, bestfit=True, estimate_ci=True,
                         line_kws={'label': 'BF Line', 'color': 'b'},
                         scatter_kws={'label': 'Observations'},
                         problabel='Probability (%)')
ax.legend(loc='lower right')
ax.set_ylim(bottom=-2, top=4)
seaborn.despine(fig)

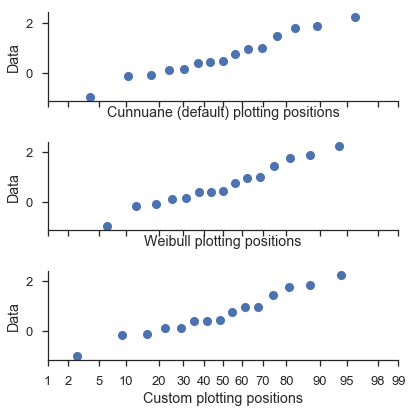
調整繪圖位置¶

probplot 函數會呼叫 viz.plot_plos() 函數來計算每個資料集的繪圖位置。

您應閱讀該函數的 docstring 以取得更多詳細資訊。但高階概述是，在繪圖位置計算中，您可以調整幾個參數（alpha 和 beta）。

最常見的值可以透過 postype 參數選取。

這些透過 probplot 中的 pp_kws 參數控制，並在下一個教學中更詳細地討論。

common_opts = dict(
    plottype='prob',
    probax='x',
    datalabel='Data',
)

numpy.random.seed(0)
x = numpy.random.normal(size=15)

fig, (ax1, ax2, ax3) = pyplot.subplots(figsize=(6, 6), nrows=3,
                                       sharey=True, sharex=True)
fig = probscale.probplot(x, ax=ax1, problabel='Cunnuane (default) plotting positions',
                         **common_opts)

fig = probscale.probplot(x, ax=ax2, problabel='Weibull plotting positions',
                         pp_kws=dict(postype='weibull'), **common_opts)

fig = probscale.probplot(x, ax=ax3, problabel='Custom plotting positions',
                         pp_kws=dict(alpha=0.6, beta=0.1), **common_opts)
ax1.set_xlim(left=1, right=99)
seaborn.despine()
fig.tight_layout()

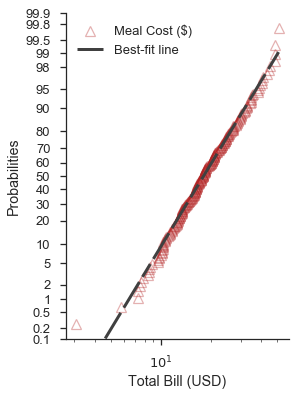
控制圖表元素的視覺效果¶

如上面的範例所示，probplot 函數採用兩個字典來自訂資料系列和最佳擬合線（分別為 scatter_kws 和 line_kws）。這些字典會直接傳遞至目前軸的 plot 方法。

依預設，資料系列會假設 linestyle='none' 和 marker='o'。這些可以透過 scatter_kws 覆寫

重新檢視之前的範例，我們可以像這樣自訂它

scatter_options = dict(
    marker='^',
    markerfacecolor='none',
    markeredgecolor='firebrick',
    markeredgewidth=1.25,
    linestyle='none',
    alpha=0.35,
    zorder=5,
    label='Meal Cost ($)'
)

line_options = dict(
    dashes=(10,2,5,2,10,2),
    color='0.25',
    linewidth=3,
    zorder=10,
    label='Best-fit line'
)

fig, ax = pyplot.subplots(figsize=(4, 6))
fig = probscale.probplot(tips['total_bill'], ax=ax, plottype='prob', probax='y', bestfit=True,
                         datascale='log', problabel='Probabilities', datalabel='Total Bill (USD)',
                         scatter_kws=scatter_options, line_kws=line_options)
ax.legend(loc='upper left')
ax.set_ylim(bottom=0.1, top=99.9)
seaborn.despine()

注意

probplot 函數可以採用兩個額外的視覺參數：color 和 label。如果提供，color 將覆寫 scatter_kws 和 line_kws 參數的標記面顏色和線條顏色選項。同樣地，散佈系列的標籤將會被明確的參數覆寫。不建議使用 color 和 label。它們主要存在是為了與 seaborn 套件相容。

將機率圖映射到 seaborn FacetGrids ¶

一般而言，probplot 的編寫考慮到了 FacetGrids。您只需要在呼叫 FacetGrid.map 時指定資料欄和其他選項即可。

不幸的是，標籤的運作方式並不如我所願，但這仍在進行中。

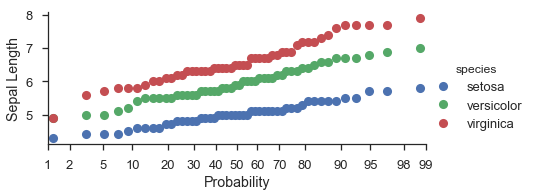
fg = (
    seaborn.FacetGrid(data=iris, hue='species', aspect=2)
        .map(probscale.probplot, 'sepal_length')
        .set_axis_labels(x_var='Probability', y_var='Sepal Length')
        .add_legend()
)

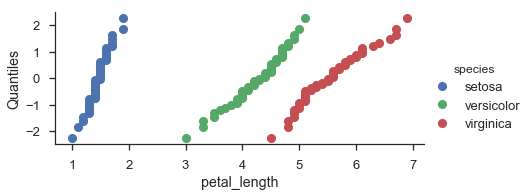
fg = (
    seaborn.FacetGrid(data=iris, hue='species', aspect=2)
        .map(probscale.probplot, 'petal_length', plottype='qq', probax='y')
        .set_ylabels('Quantiles')
        .add_legend()
)

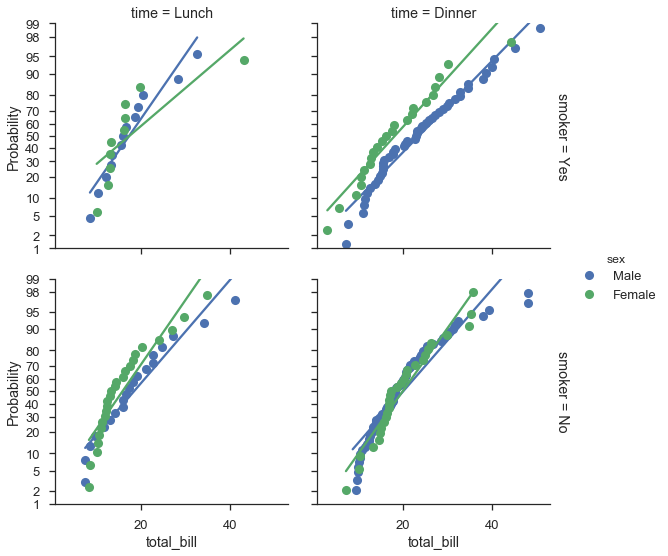
fg = (
    seaborn.FacetGrid(data=tips, hue='sex', row='smoker', col='time', margin_titles=True, size=4)
        .map(probscale.probplot, 'total_bill', probax='y', bestfit=True)
        .set_ylabels('Probability')
        .add_legend()
)